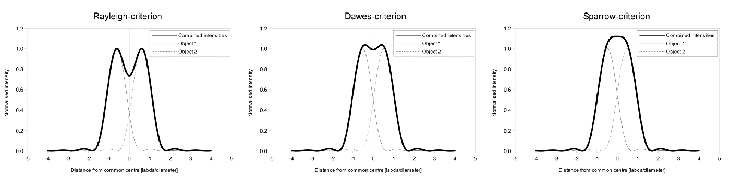
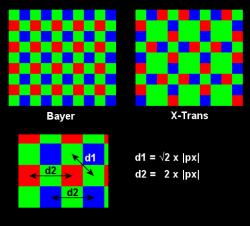
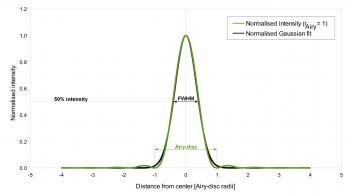
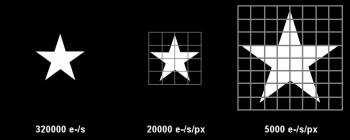
Magnification under the microscope, part 1: how to determine the optimal focal-ratio?19 September 2019 (© N. de Hilster & Starry-Night.nl) In contrast to normal photography, where the camera and lens are generally of the same brand and matched to each other, in astrophotography a telescope of any brand A is combined with a camera of any brand B. It is not uncommon for a Barlow lens of yet another brand to be placed in between. We then use this combination to take as detailed as possible images of DSOs or the Sun, Moon and planets. The images we create in this process are sometimes spectacular, but the question is whether we get the most out of our combination of camera and optics. Is the magnification not too little or is it too much? Could we have used our observing time more economically? A search on the internet yields various rules of thumb that the telescope/Barlow lens/camera combination should comply with, but the theoretical background is by no means always discussed, and the rules not always correct. In this article I hope to provide some clarity in this matter and especially in the underlying physics. In addition, I show that the current rules of thumb need to be adapted for use on color cameras. [Part 2 of this article was published on October 1, 2022 (greatly improved on December 16 that year) with a further analysis of the optimal focal ratio and addition of a testing method. It also shows that the correction for the colour camera can be ignored when stacking.] The images of the Airy discs with refraction rings in this article were all generated using PhP from the first kind of first-order Bessel function. Two gray scales have been used: one is linear, where 0% intensity corresponds to black, 100% to white and the intermediate area is 8-bit divided (256 gray values). The other gray scale is logarithmic, where again 0% corresponds to black and 100% to white, but the intermediate area is logarithmically divided according to the formula (log(intensity+1/255)*255)/log(255)*255 to make the refraction rings visible. Images 1 and 2 were generated with four refraction rings, the others with two to keep the images small. A few concepts and formulasIn fact, we can complete the calculations with a few very simple formulas and a handful of concepts: Focal ratio (f#)The focal-ratio (hereinafter referred to as f#) is the ratio between the diameter of a telescope's objective (D) and its focal length (both in the same units). In formula form this is written as: Airy-disc (rAiry)If we look through a telescope in an ideally calm atmosphere and with the eyepiece in focus, we see the stars as small discs, the so-called Airy discs (see figure 1) , surrounded by concentric circles. The Airy discs and circles are the result of diffraction through the aperture of the telescope. The Airy disc is named after Sir George Biddell Airy (1801 – 1892), the seventh Astronomer-Royal of England, although the phenomenon had already been described by Sir John Frederick William Herschel (1792 – 1871). It is a disc centred at the centre of the visible star and has a radius equal to the radius of the first diffraction dark ring that circles it. The smallest radius (rAiry) that the disc can be, depends on the wavelength of the light and the aperture of the telescope: The factor 1.22 is the angle θ (in radians) at which the first minimum of the Bessel function falls. This minimum is at x = 3.83170597, the angle θ can be calculated from θ = 3.83170597 / π = 1.2197, rounded off to 1.22. For us the on the image-chip projected Airy-disc is of interest. This projected radius, when focused correctly under an ideal atmosphere, is a measure of the smallest details we can possibly see with the telescope/camera combination. Being a small angle we may multiply [ In combination with [ For green light (λ = 540nm) [ Under ideal conditions and good focus with green light, the projected radius in micrometers (µm) of the Airy disc is therefore only dependent on the focal ratio (f#). Below we will see how this measure can be converted to the number of pixels on the image chip or seconds of arc in the sky. Rayleigh-criterium (rRayleigh)If we now look through the telescope at two objects that are very close to each other (two stars or two details on the surface of a planet), the Rayleigh criterion is the minimum mutual distance at which we can distinguish the two objects. This criterion is named after the Englishman John William Strutt FRS, 3rd Baron Rayleigh (1842 – 1919), who described it in 1879 in The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. In the case of a binary star, this means that the intensity maximum of one star lies on the intensity minimum of the other (see figure 2). This mutual distance is known to us as the Airy disc radius rAiry. The same criterion also applies to planetary details: if two parallel lines are closer than this distance from each other, it is almost impossible to distinguish them from each other. In formula form, the Rayleigh criterion is therefore very simple: Dawes and Sparrow criteria (rDawes and rSparrow) Figure 3: Dawes and Sparrow criteria compared with the Rayleigh criterion (left with logarithmic gray scale). In addition to the Rayleigh criterion, there are the Dawes and Sparrow criteria, see figure 3 and figure 4. The Dawes criterion predates the Rayleigh criterion and is named after the astronomer William Rutter Dawes (1799-1868) who described it in 1867 in Memoirs of the Royal Astronomical Society, Vol. 35.2 Dawes had determined empirically that the resolving power of a telescope was 4.56″ divided by the lens diameter in inches (about 85% of the Rayleigh criterion). However, the Rayleigh criterion was more formal, being based on the theoretical Airy-disc diameter, and was therefore gaining ground. In 1916 C.M. Sparrow published his criterion in The Astrophysical Journal with the premise that a binary star can no longer be resolved if the Airy discs overlap so much that the intensity in the overlap region remains constant (see figure 4).3 The Sparrow criterion is approximately 77% of the Rayleigh criterion. The difference between the Dawes and Sparrow criteria is barely visible in the logarithmic gray scale, but still clearly visible in the linear gray scale. Recent research has shown that these criteria no longer have to be a lower limit.4 Nyquist criterionIf we want to capture a waveform or a structure in digitization in such a way that we can reconstruct it from the digital data without losing the smallest details, then we will have to collect data with a higher resolution than the smallest details are large. According to the Nyquist criterion, this sampling resolution must be a factor of 2 higher than these smallest details to be preserved.4.1 For example, music is digitally sampled at a frequency of 44.1 kHz, so that a pitch of 22 kHz (= upper limit of our hearing) can still be reconstructed. Pixel size (|px|)This article regularly refers to the pixel size, the measurement in micrometers (µm) of a pixel on the image chip. This measure will generally be abbreviated as |px|. Camera resolutionThe camera resolution is the size of the pixels on the image chip, expressed in arcseconds (“), as a function of pixel size |px| (in µm) and the focal length f (in millimetres). In formula form this is written as: The factor 206.3 is the conversion factor to get from radians to arcseconds: 180 / π degrees per radian x 3600 arcseconds per degree = 57.296 x 3600 = 206264.8, which is again divided by 1000 because |px| is given in micrometers, so 206.2648, rounded to 206.3. Field of view (FOV)The FOV of the camera/telescope combination, expressed in minutes of arc ('), as a function of sensor size |sensor| (in millimetres) and the focal length f (in millimetres). In formula form this is written as: The factor 3438 is the conversion factor to get from radians to minutes of arc: 180 / π degrees per radian x 60 arc seconds per degree = 57.296 x 60 = 3437.76 (|sensor| is given in millimetres), rounded up to 3438. Full Width Half Maximum (FWHM)If, under an ideal atmosphere, the light of a star falls on an imaging chip, an Airy-disc will be created by diffraction. Plotting the intensity against the position along the diameter of the Airy-disc gives us more or less a Gaussian curve, also known as the normal distribution (see figure 5 for the difference between the normal distribution and the intensity curve). The diameter of the projected disc at which 50% of the maximum intensity is reached (corrected for the intensity of the background) is the Full Width Half Maximum (FWHM, see figure 5). The FWHM is generally calculated from the data, but can also be determined theoretically from the wavelength of the light, the aperture of the telescope and the focal length. This theoretical FWHM is hereafter referred to as FWHMTheoretical and is written in formula form as: In combination with [ For green light (λ = 540nm) [ Curve fitting is used to determine the FWHM from the data, where a Gaussian curve is fitted to the data as closely as possible.7 In figure 6, the red dots are the data as obtained from the camera (determined along the diameter of the star). The curve is fitted and the FWHM follows from the 50% level of the curve. HFD (and HFR)The more robust successor to FWHM is the Half Flux Diameter (HFD). The HFD is determined by determining the circle within (and outside) of which the amount of energy is 50% of the full star image (corrected for background, see figure 7).8 The energy is determined from the sum of ADU produced by the sensor.9 The method is more robust than the FWHM and handles doughnuts (annular image of a star due to being out of focus), noise and seeing (deterioration of the image due to atmospheric conditions) better than the FWHM.9.1 In addition, the method is linear (except close to focus), so that it is extremely suitable for controlling auto-focus routines. The Half Flux Radius (HFR) is also used, for which the following applies: The influence of the color cameraThe formula [ However, this does not apply to colour cameras. There is a layer of filters over the image chip. The pixels of the image chip are all monochrome, but thanks to this layer of filters, the pixels are assigned a certain fixed colour. There are several ways in which this filter layer is applied, figure 8 shows the Bayer and the X-Trans pattern thereof. With a Bayer pattern the ratio between red, green and blue pixels is 2:4:2, for an X-Trans pattern this is 2:5:2 (for the Bayer pattern this ratio can of course be simplified to 1:2:1, but for the comparison with the X-Trans pattern it was more convenient to note this as 2:4:2). Since the Bayer pattern is more general, I will not discuss the X-Trans pattern further here, all further text applies to the Bayer pattern. The smallest visible details in our images depend on the size of the Airy-disc, the Rayleigh criterion and the Nyquist criterion. It is with the latter that the Bayer pattern comes into play. In contrast to a monochrome camera, where every pixel produces data regardless of the colour filter, with a colour camera only those pixels provide data in a certain colour where they have been fitted with that type of colour filter. So if we look at green light, then half of the pixels provide data, if we look at red or blue light, then only a quarter of the pixels provide data (see figure 9). If we now look at the shortest distance between the pixels (see figure 8), we see that for red and blue this is 2 x |px| is, while for green this is √2 x |px| is. Since the red and blue pixels have the greatest centre-to-centre distance, they limit the camera's maximum achievable resolution (unless we're going to use it monochrome for green light). This means that the effective resolution of a colour camera is 2 x |px| and that we must take this into account in our calculations and operations. In order for a 2-megapixel camera to still produce a plate with 2 megapixels, the other three-quarters of the pixels (half in the case of green) are filled with interpolated data (which is therefore not real data!). A colour camera with a |px| of 2.9µm thus has the same sampling density as a monochrome camera with a |px| of 5.8µm, but the latter has the advantage that it is four times as sensitive to light as the colour camera (assuming the same quantum efficiency of the image chip and the same transmittance of the filter). The big advantage of the colour camera is that we can simultaneously collect data in red, green and blue, which makes it easier to photograph, for example, rapidly rotating planets with surface details such as Jupiter. [In Part 2 of this article, it is shown that stacking eliminates the need to account for effective resolution, but that more data is needed to achieve the same signal-to-noise ratio.] The rules of thumbNow that the theory is known, we can analyse three commonly used rules of thumb: DJupiter in px = DOTA in mmThis formula gives the maximum diameter in pixels that Jupiter should be with a telescope (OTA) with a diameter DOTA in millimetres. If Jupiter is larger, either the pixels would be too small or the f# of the aperture would be too large. The method is analysed below with two examples, the first using an 11″ f/10 SCT with a 5.86µm monochrome camera, the second using a 5″ f/5 Newton with a 2.9µm colour camera. f# = 3-5 x (|px| in µm)The f# would be directly related to |px|, being 3 to 5 times (according to some only 5 times) larger than |px| in micrometres. The method is analysed below using an example with an 11″ f/10 SCT. f# = 3-5 x FWHM/2The f# is said to have a direct relationship with FWHM, where it may be 3 to 5 times (some say again only 5 times) greater than half the FWHM in micrometers. The method is analysed below using an example with a 6″ f/7 refractor with a 3.8µm monochrome camera. The analysis of the rules of thumbUsing the theory it is now possible to test the above rules of thumb. 1) DJupiter in px = DOTA in mm [V1]This formula gives the maximum diameter in pixels that Jupiter should be with a telescope with a diameter DOTA in millimetres. An example:
According to the formula DJupiter in px = DOTA in mm, DJupiter should be a maximum of 279 pixels. Using [ Currently (August 2019) DJupiter = 41″. With the above calculated resolution of 0.43″/px Jupiter will be 41/0.43 = 95 pixels in size. Since Jupiter should be 279 pixels according to the rule of thumb, we may apply a 3 x Barlow to achieve this. Jupiter then becomes 95 x 3 = 285px (only 2% too large), the OTA then becomes f/30, which doesn't sound unreasonable. Conclusion rule-of-thumb V1 The method does not sound unreasonable, but to see whether this means that DJupiter in px = DOTA in mm is actually correct and thus generally applicable, we must first analyse the other rules of thumb. We will then further analyse this rule of thumb on the basis of a second example. 2) f# = 3-5 x (|px| in µm) [V2]The f# is said to be directly related to |px|, being 3 to 5 times (according to some only 5 times) larger than |px| in micrometres. We have seen with the concepts and formulas that all objects suffer from diffraction and that the smallest objects are imaged as an Airy-disc under ideal conditions on our imaging chip. In order for two objects to be distinguished, they must meet the Rayleigh criterion, which states that they are only distinguishable if their distance from each other is equal to the Airy-disc radius. If we want to visualize this, the Nyquist criterion states that we have to divide this distance by two. According to the Nyquist criterion, we have to divide this by 2 and thus So conversely, a 3.3µm pixel size camera should have an f/10 telescope. In other words: This at least explains the factor of 3 in the formula f# = 3-5 x (|px| in µm). But where does that factor 5 come from? Figure 10 shows us the Nyquist criterion in action. At the very top, we see an object that exactly meets the Rayleigh criterion (see figure 2). The left column shows the object in a logarithmic gray scale, the right column shows the exact same object, but in a linear gray scale. The second row shows what happens when this object is sampled with a resolution equal to the Airy disc radius (this is also a rule of thumb), which is denoted by “r/1.00”. So the two images in this row are what we can expect if an image chip is used with |px| equivalent to rAiry. Below that is is shown what happens if the Nyquist criterion is exactly met (r/2.00). The f# is now exactly 3 x |px| and yet we still see a singular object. If we go over that a fraction (r/2.04 in the image), we begin to see the contours of the Rayleigh object. Even at larger f#, the Rayleigh object remains clearly visible. In other words: in order to detect a Rayleigh object in the data, the sampling must take place at an interval of at most the Airy disc radius! For the f#, this means that it must be at least 3 x |px|, so preferably slightly larger (in the example, a factor of 3.1 is sufficient). The reason that a factor of 5 is used has remained unclear to me, but has two possible causes: Triple sampling simply assumes a Nyquist criterion with a factor of 3 instead of 2. In the example with the 11″ f/10 SCT, [ The 2D sampling correction would be necessary because the Nyquist criterion would have been developed for one-dimensional data, whereas here we are working with two-dimensional data. For this reason, not the single side should be taken as a reference, but the diagonal. So the factor 3 should be multiplied by √2, which would lead to a factor of √2 x 3 = 4.24. However, in my opinion this is not correct. If we look at the difference between CCD and CMOS sensors, we see that with CMOS sensors the entire image field is read at once, but with CCDs this goes column by column. This means that CMOS sensors actually produce a 2D image, while CCDs produce a series of one-dimensional arrays. This would mean that we would have to use a different 'Nyquist factor' for a CMOS than for a CCD, but that is obviously not the case. The same would apply for a Region Of Interest (ROI) that is only 1 pixel high or wide (or if we used a one-dimensional image chip like in a flatbed scanner). But even when we actually look at the data, we see that the Nyquist criterion holds up to rotation. Another argument for applying the 2D sampling correction would be the non-sensor alignment of the two point sources in the Rayleigh object. To sample a Rayleigh object, we must divide the distance between the two point sources by two. When the Rayleigh object is fully aligned with the sensor, only two pixels fit between the two centres. However, the Rayleigh object also has a width, but with an image perfectly aligned to the sensor, this does not matter. However, if the object rotates, this will play a role. We need to sample in the direction of the line between the two point sources, but now we have at least four pixels there in width (with a rotation of 45 degrees, this increases to 6 pixels). The direction of the line through the two centers is where we have to sample, so we have to see what interval there is between the perpendiculars from the pixels on this line (see figure 11)., the green line is the sampling direction, the red lines are the perpendiculars of the pixels).  Figure 12: A Rayleigh object at 45° rotation and Airy-disc radius sampling interval (linear gray scale). The image shows a Rayleigh object rotated 14 degrees relative to the sensor. Not entirely coincidentally, this is the rotation in which the perpendiculars have a constant distance from each other and a maximum achievable resolution occurs. The sampling interval is now only a quarter of the pixel size, or an eighth of the Airy disc radius. Even if we only use the brightest half of the pixels, the interval will never exceed three-quarters of a pixel, which is about a third of the Airy-disc radius. In this rotation, the Nyquist criterion is therefore amply met. The average sampling distance for rotations greater than 8 degrees is only 50% of the sampling distance for a fully aligned object. The rotation also plays a role in another way. The Pixels are square and when the Rayleigh object is rotated the corners of the pixels 'prick' inwards. This can already be seen a little in figure 11, but at the ideal rotation of 45 degrees (see figure 12), it is therefore possible to still image the Rayleigh object even with a sampling interval equal to the Airy disc radius (i.e. only half the Nyquist criterion), something that is definitely not possible without rotation. Figure 13 therefore shows that the standard Nyquist criterion holds for arbitrary 2D data. Where in figure 8 a Rayleigh object was still used that was neatly aligned with the axes of the image chip, this relationship has been abandoned in figure 13. The image consists of six groups of two columns each of Rayleigh objects. In the top row, the objects are aligned with the image chip, as in figure 6), the row below has an orientation of 15°, the one below that has an orientation of 30° and the bottom row has an orientation of 45°. The two columns are chosen in such a way that the objects are positioned differently relative to the pixel edges.  Figure 13: Nyquist criterion applied to Rayleigh objects with different orientations (logarithmic gray scale). The first group (far left) shows the original Rayleigh objects, the second group has them sampled according to the Nyquist criterion (r/2.00). It can clearly be seen that the Rayleigh object at the top right of this group is still shown as a single object, the others are already multiple. From the third group from the left (r/2.04), all Rayleigh objects are clearly multiple. The second group from the right (r/2.82) shows the objects at a sampling interval according to the proposed 2D correction, but from groups (r/2.04) and (r/2.50) it should be clear that this sampling is already more than fine enough. Figure 14 shows an animation of a ring consisting of two parts that meet the Rayleigh criterion. Both parts are constructed according to the intensity curve of an Airy disc and are spaced apart by the Airy-disc radius. The animation goes through the f# in steps, at factor 3 is the turning point, below that the rings begin to merge, first partially and then completely. The 2D sampling correction can therefore be omitted, but we must stay just above the Nyquist criterion: The analysis of this second rule of thumb has so far been based entirely on the assumption that a monochrome camera is used. We have seen earlier that the use of a colour camera has an effect. If the camera has a Bayer pattern, |px| to be multiplied by 2. Formula [ With (i) = 1 for a monochrome camera and 2 for a colour camera with a Bayer pattern. Conclusion rule-of-thumb V2 It has become clear from the above analysis that f# = 3-5 x (|px| in µm) is only partially valid. It is preferable to stay just above a factor of 3 to be able to capture Rayleigh objects in any case. The factor 5 we encounter seems to have been chosen more or less at random and is easy to remember, but it does lead to oversampling. Finally, the formula does not account for the influence of the colour camera, so it should be written as f# > 3 x (|px| in µm) x (i), where (i) = 1 for a monochrome camera and 2 for a colour camera with Bayer pattern. 3) f# = 3-5 x FWHM/2 [V3]The f# would be directly related to FWHM, being allowed to be 3 to 5 times greater than half the FWHM in micrometres. Incidentally, some also use the entire FWHM as a reference. The idea behind this method is that the FWHM is directly measured with the OTA/camera combination. So it would be a very pragmatic solution. However, this immediately provides the first counterargument for this method: The FWHM depends on a combination of factors. Basically, assuming ideal atmospheric conditions, the FWHM is completely dependent on the Airy-disc, which itself is dependent on the f# of the telescope used. So we try to determine the f# by using an f#. Of course the seeing, the quality of the optics, collimation, focus and |px| play a role also play a role in the size of the measured FWHM and together they ensure that the FWHM will always be larger than the FWHMtheoretical. From the previous section on the rule of thumb f# = 3-5 x (|px| in µm) it became clear that the sampling density should be half the Airy-disc radius. So using the whole FWHM as a reference, as is sometimes done, is incorrect (unless divided by 4). Since the FWHM is determined at the 50% intensity level, its diameter will be approximately equal to the radius of the Airy-disc (see figure 15). The method f# = 3-5 x FWHM/2 is therefore equivalent to f# = 3-5 x (|px| in µm), with the advantage of including all disturbances. It is for this reason that Chris Woodhouse wrote that “ … the FWHM and Rayleigh Criterion have similar values and can be treated as one… ”.15 Just a calculation example:
From [ If we now calculate the f# with the lowest value for FWHM from APP, we get (with the factor 5): 5 x 8.4/2 = f/21. With the maximum of the second rule of thumb (“5 x |px|”) this becomes: 5 x 3.8 = f/19, indeed similar (this would mean we could use a 3 x Barlow). Assuming the more correct formula [ Conclusion rule-of-thumb V3 Although FWHMtheoretical is approximately equivalent to rAiry and the best measured FWHM actually leads to results approaching the second rule of thumb (3-5 x |px|), the method is better suited for determining the binning factor than for determining the f#, mainly because the FWHM to be measured depends on the f#. 4) DJupiter in px = DOTA in mm [V1] (on repetition)In the first example with this formula we found an f# of 30. With the second rule of thumb (3-5 x |px|) this would be for the camera used with a |px| = 5.86µm may also be a maximum of f/30, so so far the rules of thumb are consistent. Now for a second example:
According to the formula DJupiter in px = DOTA in mm, DJupiter should be a maximum of 130 pixels. Since we are using a colour camera, the sampling interval (i) will be twice the |px|, so 5.8µm. Using [ As previously determined, DJupiter = 41″. With the just calculated resolution of 1.84″/px, Jupiter will be 41/1.84 = 22 pixels in size. While the camera will produce a frame where Jupiter is 44 pixels in diameter, half of that is actual data, the rest is interpolated. Since Jupiter should be 130 pixels according to the rule of thumb, we should use a 6 x Barlow to achieve this diameter. Jupiter then becomes 22 x 6 = 132px (only 1.5% too large), the OTA then becomes f/42. The frame the camera produces will then show a Jupiter 264 pixels in diameter, but only half of that is real data. If we still include the interpolated pixels in the calculations, we would arrive at f/21 (but that is not correct). According to the formula [ Let's return to the first example of the Jupiter rule of thumb, where we were allowed to use an f/30 scope for a monochrome camera with |px| = 5.86µm, then with formula [ Conclusion rule-of-thumb V1 (revisited) While the first example still seemed very reasonable, this second example of the Jupiter rule of thumb shows that formula [V1] is not generally applicable, but has been drawn up for a specific OTA/camera combination. With formula [ About over- and undersamplingAbove we learned how to adjust the optics to the camera (or vice versa). This will not always work very well and the last question we have to answer is how to deal with oversampling and undersampling. What are the pros and cons of both and are they really as bad as it is sometimes claimed? Figure 16 shows what happens with oversampling and undersampling. The original object can be seen at the very top, with the object directly below it as it falls on our image sensor as a result of the Airy disc. Then two situations occur: on the left there is 30% oversampled, on the right 30% undersampled. Then the images were scaled back to the one built from Airy-discs and finally these scaled back images were subtracted from the original Airy-disc version and brightened slightly to show the differences (depending on the monitor, the latter is probably only visible when the image is enlarged). The difference between oversampling and undersampling is clearly visible from the difference images. Neither of them (obviously) reproduce the original image, but the differences are much smaller with oversampling than with undersampling. So if we don't want to lose too much detail, oversampling is more sensible than undersampling. This is especially important for planetary images. If it is not too much at the expense of the shutter speed, then the advantage of oversampling is that the planet can be placed larger on the screen. However, there are also advantages to undersampling, especially in deep-sky photography. As we saw above, undersampling produces more light, while not necessarily compromising the quality of the recordings. In addition, we should always ask ourselves what we are going to use the recordings for. Recently, astrophotographer Bart Delsaert took a particularly beautiful and very successful photo of M31 in 25 hours with a 16″ f/3.75 telescope at a resolution of 9300 x 6200 pixels. There is nothing to criticize on the photo, but we may wonder what that resolution is needed for. Even a 4K Ultra HD screen (resolution 3840 x 2160) does not have enough pixels to display the photo in full resolution without zooming in. If the photo is intended for high-resolution printing (300dpi, but 72dpi is sufficient for a poster), it will be an image of 79 x 53 centimetres (or 2.4 x 2 meters at 72dpi). Of course it is wonderful that we can zoom in on our screen to see more details, but by binning (= more light gathering, so shorter exposure time) the image could have been shot in a quarter (6 hours) or a sixteenth (one and a half hours) of the time. Figure 17 shows the advantages and disadvantages of oversampling. Suppose we receive 320000 e‾ s–1 from an object and we sample it with an array of 16 pixels, that yields 20000 e‾ s–1 px–1. At 2x oversampling, this drops to 5000 e‾ s–1 px–1, but we get a 2x larger image. So it completely depends on what we want to achieve with the image whether oversampling or undersampling has any benefits. ConclusionThis article started by discussing a few concepts and formulas that are necessary to get a good idea of the magnification that a particular OTA/Camera combination produces and whether or not it leads to oversampling. The role of the camera was explored, explaining the differences between a colour and monochrome camera. This showed that the colour camera has a lower effective resolution than might be deduced at first glance from the pixel size. All things considered, images with a colour camera would first have to be reduced by a factor of 2 before the image resolution matches the sampling resolution. Three popular rules of thumb were then reviewed and analysed, which showed that the first formula, where the diameter of Jupiter in pixels should not exceed the diameter of the OTA in millimetres, was not generally applicable. The second formula, which states that the focal ratio of the OTA is related to the pixel size of the camera, was partly correct, but of the factors of 3 and 5 times the pixel size used, only the factor 3 could be traced back to physics as a lower limit. In addition, the formula does not take into account the type of camera (colour or monochrome), for which a correction factor is required in the calculations (1 for monochrome, 2 for colour). The last rule of thumb, which states that the focal ratio is related to the measured Full Width Half Maximum (FWHM) may be better for determining the binning factor than for determining the focal ratio, because the measurement necessary for the formula depends on the focal ratio. Finally, the effects of oversampling and undersampling were examined, which showed that both are not necessarily wrong and even have their advantages. Oversampling has advantages in planetary photography (where undersampling must be avoided), while undersampling can save time with deep-sky images. This article showed that the focal ratio should be at least 3 times the pixel-size, and that factor should be multiplied by 1 for a monochrome camera and by 2 for a Bayer pattern image chip to compensate for the sampling interval (i). In formula form: [On October 1, 2022, part 2 of this article was published with a further analysis of the optimal focal ratio and a testing method is also discussed. On December 26, Part 2 was further expanded to show that the sampling interval factor can be dropped for a colour camera when stacking is used.] Footnotes[1]: Suiter, pp. 12-13. [2]: Dawes, pp.158-159. [3]: Sparrow. [4]: Tsang e.a. [4.1]: Strictly speaking, the basis on which the Nyquist criterion rests is not suitable for application to 2D sampling with image chips. However, Robert Wildey has already shown in 1992 that it is justified and also substantiates this in his publication (see below). Today, the application of the Nyquist criterion to 2D sampling is widely accepted and is even used by companies such as Edmund Optics to explain the limitations of their cameras. [5]: Woodhouse, p.35. Crossley, M., “CCD arc-sec/pixel & Focal Ratio:”, http://www.wilmslowastro.com/software/formulae.htm#ARCSEC_PIXEL. This is similar to what is used in Stellarium 0.18.2. The term 206.3 arises from the number of arcseconds per radian: 180/π x 60 x 60 = 206265. Because |px| is given in µm and f in mm, this number must be divided by 1000. The result of the formula is in arcseconds per pixel. [6]: Moore, S., “What is the best pixel size?”, http://www.stanmooreastro.com/pixel_size.htm. For the theoretical value, see https://www.telescope-optics.net/diffraction_image.htm. [7]: Carsten, “Night sky image processing – Part 5: Measuring FWHM of a star using curve fitting – A Simple C++ implementation”, In: Lost infinity, Reaching for the stars, https://www.lost-infinity.com/night-sky-image-processing-part-5-measuring-fwhm-of-a-star-using-curve-fitting-a-simple-c-implementation/ [8]: Carsten, “Night sky image processing – Part 6: Measuring the Half Flux Diameter (HFD) of a star – A Simple C++ implementation”, In: Lost infinity, Reaching for the stars, https://www.lost-infinity.com/night-sky-image-processing-part-6-measuring-the-half-flux-diameter-hfd-of-a-star-a-simple-c-implementation/. Miyashita, K., “Half Flux Diameter: -Applicate to determination for faint star event-”, http://www005.upp.so-net.ne.jp/k_miyash/occ02/halffluxdiameter/halffluxdiameter_en.html Diffraction Limited, “Half-Flux Diameter (HFD)”, http://www.diffractionlimited.com/help/maximdl/Half-Flux.htm [9]: ADU = Analog to Digital Unit, also known as DN: Digital Number. However, these two values are not necessarily the same. The ADU depends on the ADC (Analog to Digital Converter) in the camera. A ZWO ASI1600MM Cool has a 12-bit ADC, while SGP or NINA stores the data as 16-bit, so a conversion takes place. If the data is processed with PixInsight, pixel values are displayed in 16-bit DN. Masters made in APP with this camera, can be chosen that they are saved as 32-bit masters and a conversion is again necessary. [9.1]: For the combined effect of seeing and objective size, see Hilster & Werf. [10]: Stargazing in the City (Rhea), “Jupiter (with animation) and Saturn 29/30 June 2019”, www.Astroforum.nl, 03-07-19, 13:08. [12]: Of course we can calculate this for all f# as well. According to [2.3] rAiry = 0.66 xf#. According to the Nyquist criterion, we need to divide rAiry in half to get |px| to get, so |px| = rAiry / 2 = (0.66 xf#) / 2 = 0.33 xf#. Conversely, f# = 1 / 0.33 x |px| = 3 x |px|. [13]: Crossley, M., “CCD Planetary Critical Sampling”, http://www.wilmslowastro.com/software/formulae.htm#CCD_Sampling [14]: It has been suggested that in a 2D array the sampling frequency should be multiplied by √2, see for example Woodhouse, p.35, but with his comment “Classical (Nyquist) sampling theorems might suggest two pixels are required to resolve a pair of stars but experts settle on a number closer to 3.3 adjacent pixels to guarantee the resolution of two points. (Stars do not always align themselves conveniently with the sensor grid.” (my emphasis) he seems unconvinced, especially since no reference is given for this. In critical applications (both contractual and financial) such as LIDAR Topographic Surveying, however, the factor 2 is generally maintained and at most increased in order to capture objects partially hidden under vegetation (Triglav Cekada et al: 406-411). The simulation shown above is also a strong indication that the correction is not necessary. [15]: Woodhouse, p.33. BibliographyDawes, R.W., “Catalogue of Micrometrical Measurements of Double Stars”, in Memoirs of the Royal Astronomical Society, Vol. 35, pp.137-502. Bibcode: 1867MmRAS..35..137D. Hilster, N. de, Werf, S. van der, “The effect of aperture and seeing on the visibility of sunspots when using early modern and modern telescopes of modest size”, (Castricum/Roden, 2022), doi:arXiv:2208.07244. Lord Rayleigh, F.R.S., “Investigations in optics, with special reference to the spectroscope”, in: Philosophical Magazine. 5. 8 (49), pp.261-274. doi:10.1080/14786447908639684. Smith, G.H., Ceragioli, R., Berry, R., Telescopes, Eyepieces, Astrographs: Design, Analysis and Performance of Modern Astronomical Optics, (Richmond (VA), 2012). Sparrow, C. M. (1916). “On Spectroscopic Resolving Power”, in: The Astrophysical Journal. 44: 76, pp.76-86, doi:10.1086/142271. Suiter, H.R., Star Testing Astronomical Telescopes: A manual for optical evaluation and adjustment, (Richmond (VA), 2013). Triglav Cekada, M., Crosilla, F., Fras, M., (2010). “Theoretical LiDAR point density for topographic mapping in the largest scales.”, in: Geodetski Vestnik. 54, pp.403-416. (10.15292/geodetski-vestnik.2010.03.389-402), http://www.geodetski-vestnik.com/54/3/gv54-3_403-416.pdf. Tsang, M., Nair, R., Lu, X.M., “Quantum Theory of Superresolution for Two Incoherent Optical Point Sources”, in: Physical Review X 6, 2016, https://journals.aps.org/prx/pdf/10.1103/PhysRevX.6.031033 Wildey, R.L., ‘The Nyquist Criterion in CCD Photometry for Surface Brightness’, in: Publications of the Astronomical Society of the Pacific, vol.104, (1992), pp. 285-289, http://adsabs.harvard.edu/pdf/1992PASP..104..285W Woodhouse, C., The Astrophotography Manual: A practical and Scientific Approach to Deep Sky Imaging, (New York, Oxon, 2017). If you have any questions and/or remarks please let me know. |
InFINNity Deck... Astrophotography... Astro-Software... Astro Reach-out... Equipment... White papers...
Hardware... Imaging...
Imaging artefacts Optimal focal ratio (part 1) Optimal focal ratio (part 2) Solar imaging (part 1) Solar imaging (part 2) Solar imaging (part 3)