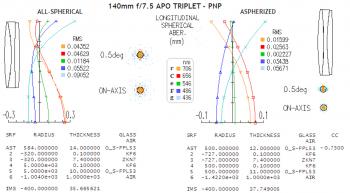
The influence of filters and objective on the focal length19 September 2021 (© N. de Hilster & Starry-Night.nl) Time can be saved in astrophotography by always focusing with the luminance filter. However, the focal length of a telescope depends on the wavelength of the light captured in the image, in combination with the quality of the objective-lens and the thickness of the filters used. If filters are used, it is therefore important to test this for the combination of the telescope and filters used. Any differences in focus distance can then be used as filter offsets and used in the acquisition software. This article is about the influence of both the telescope and the filters on the focal length, using the results of measurements with a SkyWatcher Esprit 150ED in combination with ZWO 36mm unmounted filters.  Figure 1: The spectral bandwidths of the ZWO LRGB filters used in this article (source: ZWO website). The luminance filter used for this article originates from the Chinese manufacturer ZWO and has a bandwidth (FWHM) of approximately 308nm, which corresponds to the combined bandwidth of the red, green and blue filters from the same manufacturer (see black graph in figure 1).1 The filters for red, green and blue have a bandwidth of approximately 107nm, 83nm and 111nm respectively, while for the H-alpha, O-III and S-II narrowband filters this is specified as 7nm with a margin of plus and minus half a nanometre (see figure 2).2 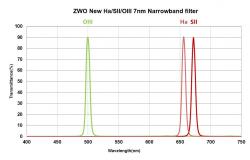 Figure 2: The spectral bandwidths of the ZWO narrowband filters used in this article (source: ZWO website). The required exposure times are inversely proportional to the relative bandwidth. A narrowband filter with a bandwidth of 7nm therefore results in an exposure time approximately 45 times longer than the 308nm wide luminance filter, while this is approximately 3 times longer for the RGB filters.3 It is for this reason that focusing is preferably carried out with the luminance filter. Now, however, there are two factors that affect focal length when using multiple filters: the thickness of the filters and the quality of the objective. Filter thicknessThe ZWO filters used here have a thickness of 2 millimetres with a tolerance of 0.03mm.4 This thickness causes the focus point to shift backwards (i.e. towards the camera). In the case of a plane-parallel glass plate, this shift depends on the glass thickness t and refractive index n (see figure 3). Assuming n = 1.5168 (Schott N-BK7 glass), we arrive at a shift s of 0.68mm, approximately one third of the thickness of the glass. The tolerance of 0.03mm specified by ZWO ensures a maximum uncertainty in that shift of plus and minus 0.01mm, so a total range of 0.02mm. The extent to which this measure is significant is further explained below. ObjectiveIn an ideal world, all light rays, regardless of wavelength, come into focus at the same location. In reality, however, there is no perfect objective, so not all wavelengths come into focus at the same focus position. Figure 4 shows for four types of refractors (the single lens or singlet, the achromat, the apochromat and the superachromat) the longitudinal aberration (the deviation of the focus point per wavelength from the mean). The vertical line with value 0 is the plane of focus, the horizontal axis shows the focus error relative to that plane (in arbitrary units). The vertical axis is the wavelength of the light and runs from UV (400nm) to infrared (900nm). Since in the ideal telescope all wavelengths would come into focus at the same focus position, such a telescope would thus produce a straight vertical graph that would coincide with the vertical 0-value line (0 on the horizontal axis). In reality there is no ideal telescope, but to approach that ideal situation, different types of lenses have been developed in addition to the singlet. The singlet ("1. Simple lens" in the figure) is unable to focus multiple wavelengths at the same position, but focuses the colours of the spectrum in their physical order. So there is always only 1 wavelength in focus (intersection of the blue line with the vertical 0-line). The achromat (green line in the graph) is able to focus two wavelengths, in the image they are blue (approximately 475nm) and red (approximately 650nm). The apochromat (APO) does this for a maximum of three wavelengths (here approximately 440nm, 650nm and 775nm) and the superachromat does this for a maximum of four wavelengths (here 430nm, 575nm, 770nm and 875nm). The difference between an achromat and apochromat is purely in the difference between two and three points of intersection, so independent of the number of elements in the objective. Now suppose we use the red, green and blue filters with the achromat from figure 4, we will then see that red and blue yield approximately the same focal length, but green does not (in the image that point is just over 4 units to the left). At the APO, blue and green are one to two units to the right when red is in focus. With the superachromat, all focus positions are between -1 and +1 units. Since the filters ensure that only that part of the graph that lies within the bandwidth of the filter is used for focusing, the quality of the lens also determines the filter offsets. With an apochromat with aspherical lenses, the differences between the wavelengths can be less than about 0.08 mm (see figure 5).5 We will now see whether this is significant. What is Significant? We have seen above that the glass thickness of the ZWO filters can vary by plus and minus 0.03mm, which can cause a focal deviation of plus and minus 0.01mm. An apochromat, such as the one used here, can add approximately 0.08mm to this due to its design. For convenience, we can assume differences of up to 0.1mm. To know if this is significant, we need to look at the Depth of Focus (DOF) and the focusing resolution of the focus motor. Depth of Focus (DOF) The Depth of Focus is the area within which focusing does not significantly improve image sharpness (so turning the focuser in and out makes no difference) and depends on the wavelength and focal-ratio of the telescope (see figure 6). The DOF is given as: With λ the wavelength of the light in nanometres, f# the focal ratio of the objective, and the result in millimetres. Of the f# the part below the fraction is used, so 7 for an f/7 telescope. For green light (550nm), the DOF is 4 x 0.00055 x 7˛ = 0.108 millimetres. This 0.108mm is the distance between the positions at which the intrafocal and extrafocal image produce more than a quarter wavelength wavefront error, so half of it (0.054mm) is the distance from the correct focus point to the point where the telescope produces more than a quarter wavelength wavefront error. It follows from the formula that with fast telescopes the DOF is smaller than with slow ones. With an f/10 telescope, the DOF is 0.220mm, while for an f/5 telescope this is only 0.055mm. This means that with a fast telescope, filter offsets will be more important than with a slow one. Focus resolution The focus resolution is the minimum step size that the focus motor can give to the focuser. The Esprit 150ED used for this article has a Starizona MicroTouch focus motor that operates the focuser at 300 steps per full turn of the fine focus knob. The Esprit is standard equipped with a 1:11 reduction, but I replaced it almost immediately with a 1:16 one. So it takes 4800 steps to give the focuser a full turn. Due to the transfer of the focus knob via a rack and pinion to the focus tube, this means that in practice approximately 172 steps are required to move the focuser 1mm, a resolution of 0.0058mm per step. As described above, the tolerance of the glass thickness of the filters can cause the focal length to shift plus and minus 0.01mm, which corresponds to approximately 4 steps with this motor-focuser. The longitudinal aberration of 0.08mm caused by the objective corresponds to approximately 14 steps. We can therefore say that the focuser has a sufficiently high resolution to compensate for the expected differences in focal length of 0.1mm. In addition, the DOF of the telescope used here is that small that the expected differences can indeed have a significant influence. We will now see whether these differences are also measurable. To measure is to knowAssuming that the expected differences are indeed significant with respect to the focuser and objective used, I performed a number of calibration measurements with the seven ZWO filters mentioned above. To simplify this process, Stanley Dimant has written a plug-in for NINA with the somewhat confusing name DarksCustoms. The current functionality, the Filter Offset Calculator, is the first of a series of functionality in this plug-in. The Filter Offset Calculator automates taking focus runs with the various filters. By default, all filters are used three times for this, the plug-in therefore focuses for all filters L, R, G, B, H-alpha, O-III and S-II, starts again at L etc. and repeats that three times by default. The number of repetitions is adjustable, so that a higher accuracy is achievable. At the end of those iterations, the plug-in shows the average focus positions at which the image was sharp for each filter and also allows it to be shown relative (see figure 7). Unfortunately, the plug-in does not indicate the accuracy achieved, so we do not know whether there are outliers between the measurements and how large they are in that case. Inquiries with Dimant learned that he does not intend to implement this. In order to get a good indication of the achievable accuracy, I decided to do 10 measurements with the plug-in with the default setting of 3 repetitions. Each measurement takes approximately 45 minutes, at the end of which the calculated results are shown as in figure 7. This means that the 10 measurements each have to be started and handled manually and are therefore not fully automatic. It took a total of four evenings to collect the required data. The values produced by the plug-in have been processed in a spreadsheet to provide more insight into the quality of the measurements. Figure 8 shows the measured offsets and the averages per filter. The colours of the measurements have been chosen in such a way that it is clear which measurements were made on the same evening. The black bars are the averages of the 10 measurements. In order to also provide insight into the quality of the measurements, figure 9 shows the means, but now with their standard deviations (at 1σ, 68% confidence level) as a bar around the means. Since the measurements for the luminance filter are normalized, the measurements would result in an uncertainty of 0 steps for this filter. In order to be able to say something about the quality of the measurements with this filter, I normalized the 10 measurements by determining the average over all filters per measurement and taking the standard deviation of these 10 averages. As shown in figure 9, there are indeed differences between the filters. The extreme values are approximately 11 steps of the motor focuser, which corresponds to approximately 0.06mm. This means that in my case both the telescope and the filters are of very good quality and this combination is virtually parfocal for all filters used. This also explains why I never noticed any blur in my images, when I simply assumed my system was parfocal. The deviation of the O-III filter from the luminance filter is about the same as the DOF and is therefore still worth adjusting. It is also striking that the measurements show that the results are not constant and that considerable differences can even occur on a single evening. Now, the weather conditions during the measurements with varying clouds and even thin stratus were not ideal, but typical for an evening when these kinds of measurements are made (in perfectly clear weather one would start imaging). We can therefore assume that differences can also be observed within the measurements, so it is to be hoped that the author of the plug-in will nevertheless decide to build in quality indicators. ConclusionIn this article I have looked at the influence of the objective lens and filters on the focal length. It has been shown that the quality of the objective (i.e. whether it is a single lens, an achromat, apochromat or super-achromat) and the thickness of the filters both, and in combination, determine the position of the focus point. When filters are called parfocal, it just means that they are about the same thickness, with ZWO this is within plus and minus 0.03mm. With a singlet or an achromat, parfocal filters cannot prevent the need for filter correction if you want to focus with the luminance filter. This is less likely to be the case for an apochromat or super-achromat, although more data is needed to substantiate this. Fast telescopes, because of their smaller Depth of Focus (DOF), are more likely to suffer from focus point shift than slow telescopes. The test with the f/7 SkyWatcher Esprit 150ED (focal length 1050mm) showed that, in combination with the used ZWO filter set, it is almost parfocal. But even though the results presented here are very good, this does not mean that with other combinations of telescopes and filters it still is likely that, when parfocal filters are purchased, the entire system will be parfocal. Owners of fast and/or achromatic telescopes in particular would do well to check this. Footnotes[1]: The bandwidths for the LRGB filters are measured in the graph of ZWO and may differ slightly in reality. [2]: ZWO, "ZWO LRGB 36mm filters", in: https://astronomy-imaging-camera.com/product/zwo-lrgb-36mm-filters and ZWO, "ZWO new narrowband 36mm filter", in: https://astronomy-imaging-camera.com/product/zwo-new-narrowband-36mm-filter, last consulted on September 17, 2021. [3]: In both cases, based on a light source that has the same intensity over the entire bandwidth and no losses occur in the optical train. [4]: ZWO, "ZWO new narrowband 1.25″ filter", in: https://astronomy-imaging-camera.com/product/zwo-new-narrowband-1-25-filter, last accessed 17 September 2021. [5]: See "Aspherical 140mm f/7.5 APO Triplet – PNP" at https://www.telescope-optics.net/semiapo_and_apo_examples.htm, last accessed 17 September 2021. [6]: TelescopeOptics.net, "9.2.1. Semi-apo and apo lens objective examples", in: https://www.telescope-optics.net/semiapo_and_apo_examples.htm, last accessed 17 September 2021. If you have any questions and/or remarks please let me know. |
InFINNity Deck... Astrophotography... Astro-Software... Astro Reach-out... Equipment... White papers...
Hardware... Imaging...
Balancing system Camera centring errors Collimator construction Dome Azimuth Calculation Filter focus-offsets RC Collimation Removing lens artefacts Removing Newton-rings Solar Seeing Monitor (DIY) Stability measurements Sun Avoidance Monitor